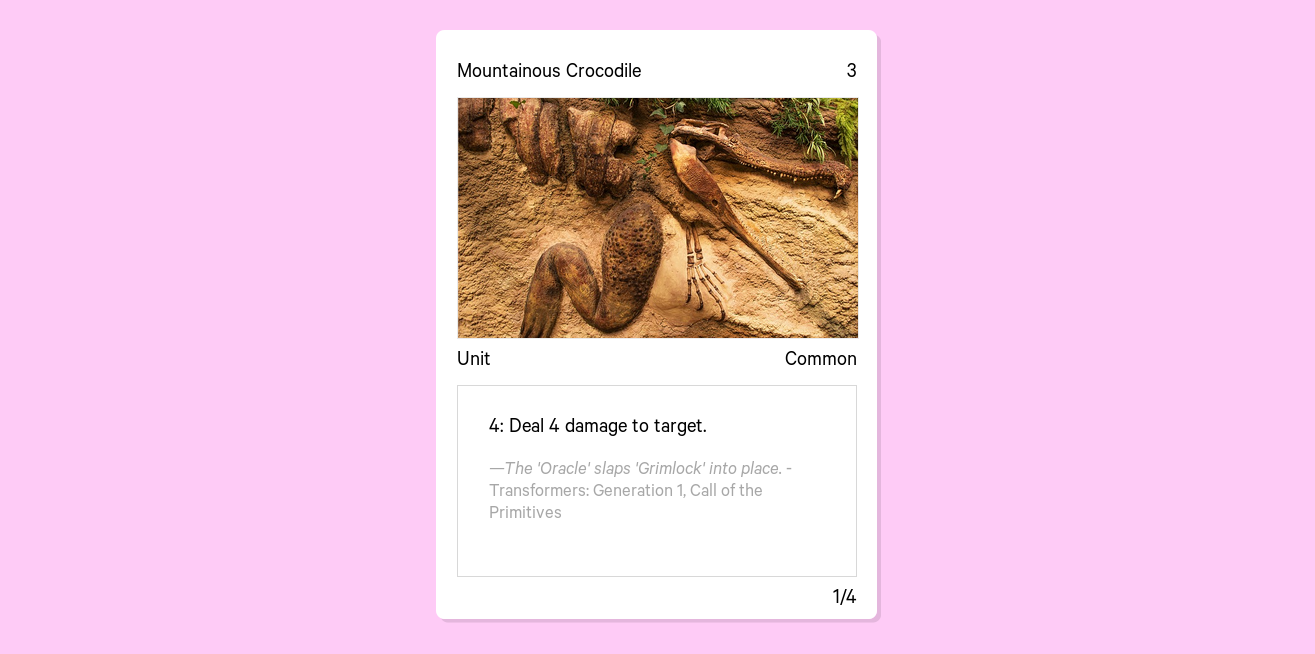
The Infinite Card Game

Kira and I were in Australia most of last month, and near where we were staying in Melbourne was a game shop. We had a free Friday night so I stopped by for my first Magic: The Gathering (MTG) draft event, and it got me thinking about designing card game systems.

MTG is a collectible card game with a great deal of strategic depth. Games with large state spaces like Chess and more recently Go have been more-or-less "solved"¹; The state space of MTG is certainly orders of magnitude larger than Chess and Go, given the massive back catalog of cards (going back to 1993!)² and the ever-growing number of interactions between them. Though the state space of Starcraft is likely larger (and people are working on "solving" it), to my knowledge MTG has not yet been solved in this sense.

For those unfamiliar with MTG, it's played between two or more players and involved constructing a deck of cards around a particular strategy. Some strategies may emphasize fast, aggressive plays ("aggro") which, if failing to win quickly, lose steam in longer matches. Others may focus on slowing opponents down by stopping plays short or making actions more expensive ("control"). And there are other strategies still.

MTG has a variety of game formats which govern how decks are constructed and can affect other game rules. These formats are broadly divided into Constructed and Limited formats. Constructed formats are where players carefully design and assemble their decks in advance. This gives plenty of space for creative, expressive strategies since players have a large pool of cards to select from. In contrast, Limited formats mean that players are given a small amount of random cards drawn from a set of cards and need to assemble a deck on-the-spot (a process called "drafting").

I've mostly played Constructed formats, but now that I've tried Limited a bit more I'm coming to prefer the randomness and uncertainty of Limited formats. In Limited you have to think on your feet more, design your deck more delicately (you aren't sure what to expect from your opponents), and work within a tighter set of constraints. It makes for more challenging and exciting games.

The problem with Limited is that each set has roughly 200-300 cards. After a few games you'll be familiar with every card and players have learned the strategies that work best within that set. Games start to get formulaic and stale. It loses that sense of uncertainty that makes Limited exciting in the first place. It isn't until the next set is released, with new cards and abilities, that things are interesting again.

These sets are carefully designed such that the cards have enough variation to keep things interesting, but not so much that they're totally incoherent (Mark Rosewater, the lead designer of MTG, has a great podcast delving into this design process). And they are meticulously balanced so no strategy is strictly better than any others.

That being said...I wonder if there's a way to design an infinite set, i.e. a dynamic and self-adjusting process which outputs a stream of cards to draw from for a never-ending Limited format. Such a system would need some rule scaffolding or framework (doesn't have to be MTG's) from which it can derive new mechanics and costs (some quantifier of their power), and then generate a balance of cards over some probability distribution.

For example, a core mechanic in MTG is that you have creatures that can attack opponents to damage them. Players can use their own creatures to "block" opponents' attacking creatures. These creatures have some cost to play ("cast") them; generally stronger creatures have the drawback of costing more to cast. Sometimes they may have other abilities which make them more or less versatile, which is compensated by a respective increase or decrease in casting cost. Sometimes you have creatures which are disproportionately cheap in casting cost for their strength, but these are rare.

Let's say the game for this infinite draft system has just this simple attacking-creature mechanic. Our creatures have only a strength and a casting cost. Generally, the stronger the creature, the higher it's casting cost. But not always — on rare occasions we might have a strong creature that's a bit cheaper than normal. Finally, we add the additional constraint that weaker creatures are more likely, so we emphasize strong creatures as a more notable event.

What we're essentially saying is that the casting cost of a creature is dependent on its strength (and vice versa), which we can represent as a simple Bayes net:

When we want to create a new card, we can first sample its strength, then sampling a casting cost depending on the value we sampled for its strength.

We want a creature's strength to be a positive integer, say in the range ¦[1, 12]¦. So we want a discrete probability distribution with finite support. We could use a Beta-binomial distribution, e.g. ¦\text{BetaBinomial}(\alpha=2, \beta=6, n=12)¦, which has the properties we want:

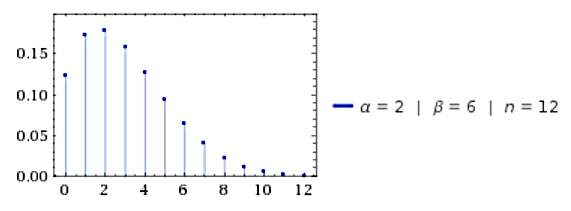
Here creatures will tend to have a strength somewhere in ¦[1, 4]¦ and very rarely above 6. Then we can do something similar with casting cost, except that it's dependent on the strength.

This is an extremely simple game and so not a very interesting one. We'd want to add in additional abilities that interact in interesting ways. For example, in MTG the "flying" ability makes a creature blockable only by other creatures with flying. So we can add in some small probability of a creature gaining flying, and have that also affect the casting cost's distribution.

A really nice version of this system is one where you can pass in an arbitrary network relating costs and abilities (a more complex example of the one above), and it would output card descriptions in some interchange form (e.g. JSON), and you can use that to print cards with whatever design you wanted.

A few years ago I prototyped a similar system of cost-based card generation, which incorporated different card types beyond creatures (which I called "units"), additional abilities, and procedurally-generated names.

This prototype doesn't incorporate intra-card balance beyond what falls out of cost-balanced cards. The relative effectiveness of various abilities are really hard to objectively quantify, since their costs are really relative to what the dominant strategies are, i.e. the metagame. So ideally this infinite draft system not only generates balanced cards but also tracks how people are playing them to learn which strategies seem over or underpowered, and correspondingly tweaks the costs of abilities related to those strategies.

The generation features I just described are more about balance but another interesting feature would be introducing a balance-drift so that gameplay never stagnates in an equilibrium of strategies. Perhaps once balance is achieved the system can gradually and temporarily bias the game towards different strategies to encourage different kinds of gameplay. That way there'd be an ebb-and-flow that keeps things interesting in the aggregate and subtly changing the overall feeling of the game.

For example, if the system sees that players almost exclusively play low-strength, cheap creatures, and almost no larger creatures, maybe it will start to slightly cheapen the larger creatures so they see more play. That in turn may cause a new strategy to dominate, maybe a slower gameplay with larger creatures, and eventually a different change would be introduced to shock the system to a different strategy equilibrium.

I've given a very hand-wavy outline of this system here and as described it by no means would match MTG's hand-designed depth and complexity. But I do like the idea of a general system where you input some mechanics and it outputs a series of cards to play a game with. You could, perhaps, model many different systems via a card game format this way.