This is the written reference for a talk at the Digital Humanities + Data Journalism Symposium in September 2016 (the slides are here). A class based on the topics presented here is now at the New School.

The world is very complex of course and seems inexorable in its acceleration of this complexity. Problems we face expand in difficulty in that they 1) grow to impossible scales but 2) simultaneously become increasingly sensitive to the smallest detail.

In 1973 Rittel & Webber described such problems as "wicked". Their paper Dilemmas in a general theory of planning attempts to enumerate the characteristics of such problems, which include but are not limited to:

• difficult to agree on the problem (or whether there's a problem at all)
• there is no comprehensive perspective
• wicked problems are interconnected
• no way to verify or experiment solutions
• there may be (very) delayed feedback loops
• every wicked problem is unique
• are nonlinear (outputs are disproportionate to the inputs)
• cannot be reduced to its parts (i.e. emergent)
• they are massive & intimidating

For example, consider the issue of climate change:

• Some people don't agree that climate change in general is an issue, some people think it's happening but it isn't caused by people, and so on.
• No individual or organization really has a complete understanding of the issue. There isn't even a single unifying perspective since it affects different communities in very different ways.
• It's deeply entangled with many other problems, e.g. displacement of populations, economic crises, ecological destabilization, globalization, etc
• We can't really experiment with solutions because the problem is so complex it's unlikely we'll ever be able to establish any convincing causal relation between the intervention and the outcome.
• Any intervention may change the nature of the problem such that we'd be dealing with a completely different problem, so any learnings from the intervention might be obsolete.
• The feedback delay between an intervention and its outcome may not be felt until years or decades later.
• Nonlinear dynamics like tipping points
• Global scale, many moving parts, many different interests, varying degrees of cooperation, etc...it is, as Emily Eliza Scott puts it, "multiscalar, multitemporal, multidimensional, and multidisciplinary"

I was listening to an interview with the philosopher Frithjof Bergmann who's involved in a project called New Work. In the interview he put forward a claim that every problem can be traced back to our relationship with work. I was skeptical at first but after some thought there is a plausible causal chain between jobs and climate change. Employment and "job creation" are of course major political issues. Some part of this probably involves manufacturing (though perhaps in decreasing amounts in more developed economies) which requires stoking the flames of consumption to keep demand up; this kind of production drives energy usage and pollution and waste which end up contributing to climate change.

It seems that although technology is often responsible for the exacerbation of such problems and their complexity, there should also be some means of technologically mitigating them. Not solve them outright — that takes much more than just new tech — but at least better equip us to do so ourselves.

I think simulation has some potential to help here.

Simulation requires that we formalize our mental models; they are a "working memory" that support larger such models, the process of designing a simulation can lead to increase understanding, at the very least identify gaps in our knowledge, and they provide a canvas for us to sketch out possible alternatives.

What simulation?

There are many different forms simulation can take. Here I'm referring to both agent-based modeling and system dynamics (i.e. causal loop diagrams) and focusing on their applications to social systems ("social simulation").

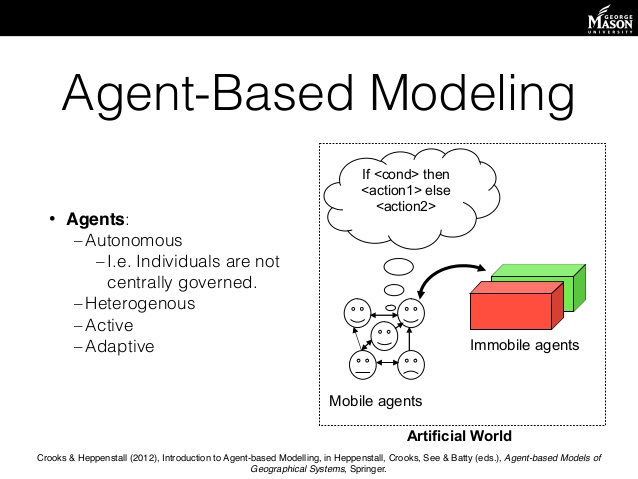
Agent-based modeling (ABM) is a method which models systems via modeling its constituent elements (e.g. people) and describing how they interact. It's often contrasted with equation-based modeling (i.e. differential equations) which is far more common but limited by assumptions hard-coded into it:

• usually assumes homogeneous population
• usually continuous variables
• cannot observe local detail, generally focuses only on aggregate phenomena
• top-down (from global perspective as opposed to individual)

Agent-based modeling, on the other hand, supports heterogeneity, is flexible in the variables it supports (discrete or continuous), provides views at both the local and global level, allows for learning/adaptive agents, and more.

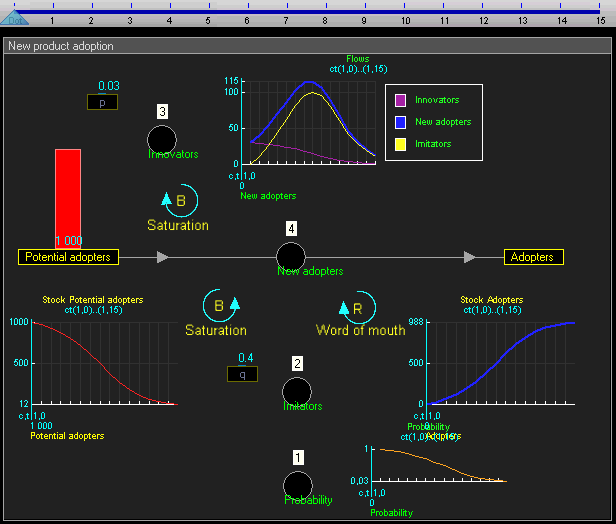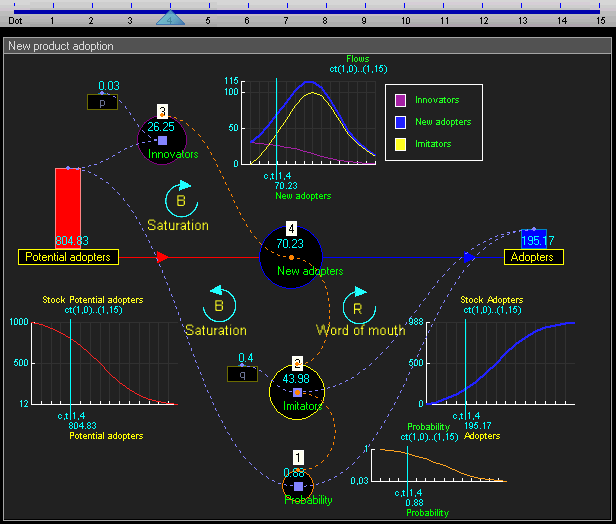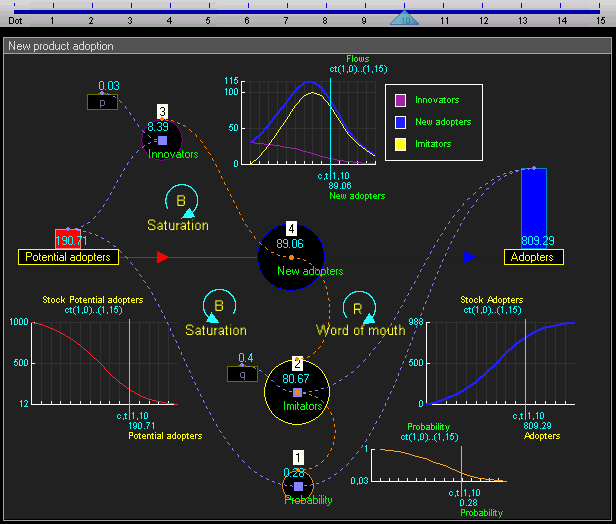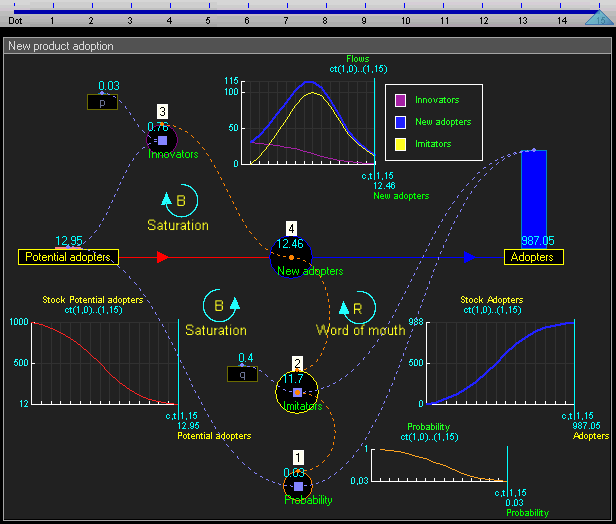
System dynamics models systems by stocks (quantities that change over time) and flows (rates of change relating stocks). System dynamics is like a higher-level abstraction over agent-based modeling, in which we don't represent individuals in a population explicitly but instead as aggregates.

An especially appealing aspect of both ABMs and system dynamics that they are much more intuitive than differential equations (I feel bad leveraging our education system's inability to make people comfortable with math, but oh well), so they are more immediately accessible to a wider audience.

They are also exceptionally flexible in what they can represent, ranging from ant colonies to forest fires to urban segregation to religious experiences.

Examples

This simulation shows how a language could evolve over time by exchanging vocabulary with random mutations.

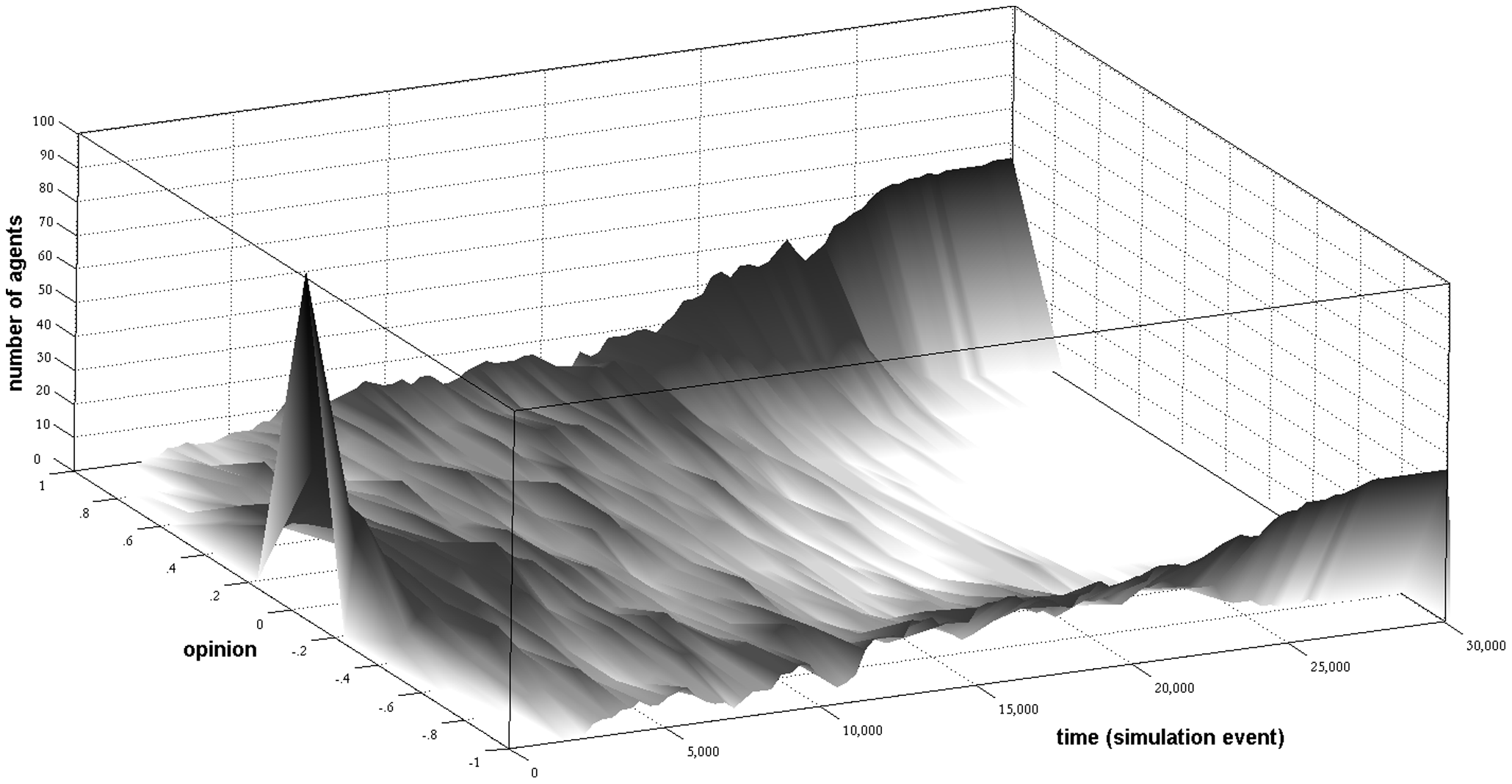
This study looks at how opinions may become polarized without requiring negative influence ("individuals’ striving to amplify differences to disliked others"). In the image you see everyone starting from the same intermediate position and eventually becoming bi-polarized.

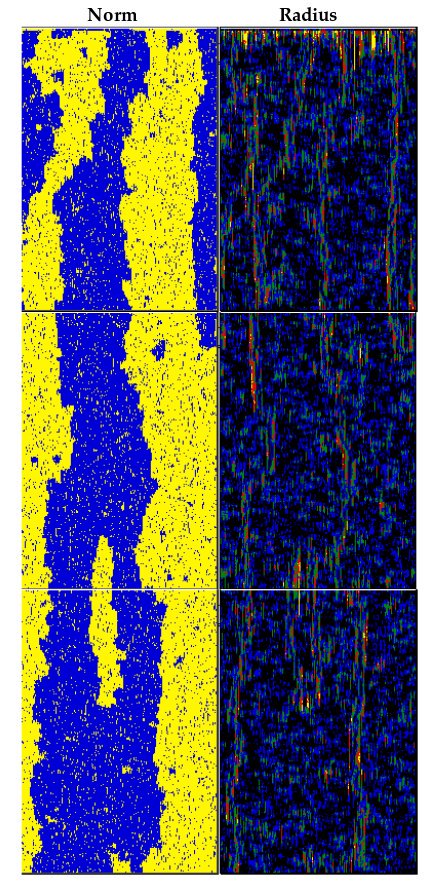
This paper models how individuals not only learn which social norms to adopt but also learn how much to think about adopting a social norm (e.g. if a social norm is prevalent enough we may adopt it without consciously deciding to). On the left, the blue and yellow colors indicate a binary norm, and the image depicts, from top to bottom, how the adoption of those norms ebb over time. There are always little pockets of resistance (e.g. yellow amongst majority blue) that eventually bloom into the new majority and eventually fall to the same fate.

This model describes how opinions shift according to social influence. I really like that this model was printed out like this.

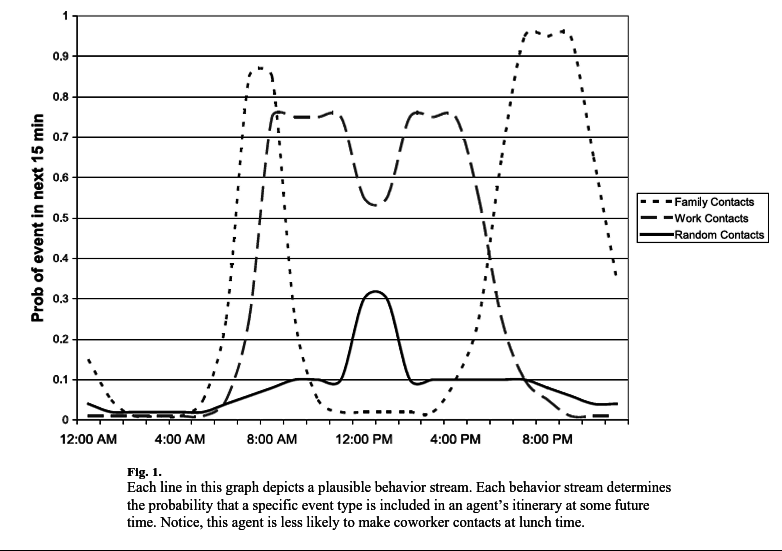
This is a massive epidemiology model at a self-described "global-scale" of 6 billion agents, running in reasonable time. This particular study models the H1N1 (swine flu) virus.

The Simulados project models hunter-gatherer groups in India from the years 10000BC to 2000BC. It's part of a broader initiative, Simulpast, which "aims to develop an...interdisciplinary methodological framework to model and simulate ancient societies".

Paradox Interactive's Cities: Skylines (similar to SimCity) models their citizen's activities as an agent-based model.

A non-digital example, MONIAC is a hydraulic system dynamics model of the UK economy.

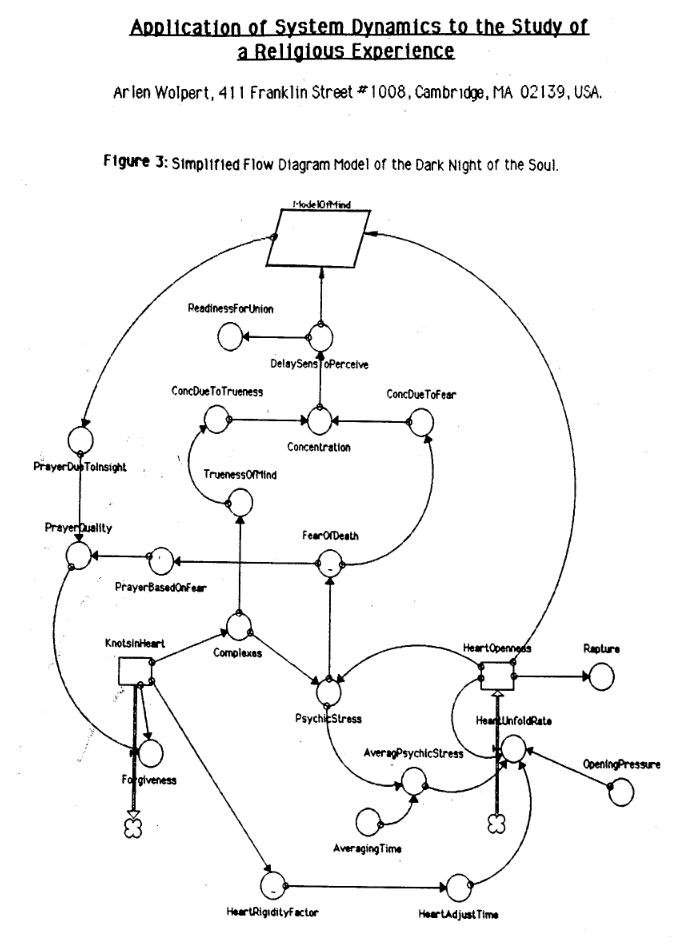
Arlen Wolpert was an engineer and a scholar of religion who used system dynamics to describe a powerful religious experience he had. I like this example because it demonstrates the method's breadth of applicability, and it's really curious to see how he framed the different components of the experience.

Agent-based modeling in more detail

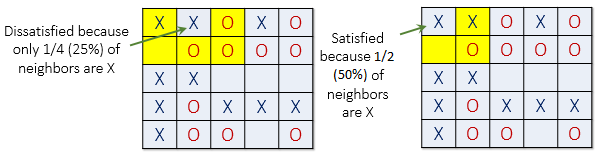
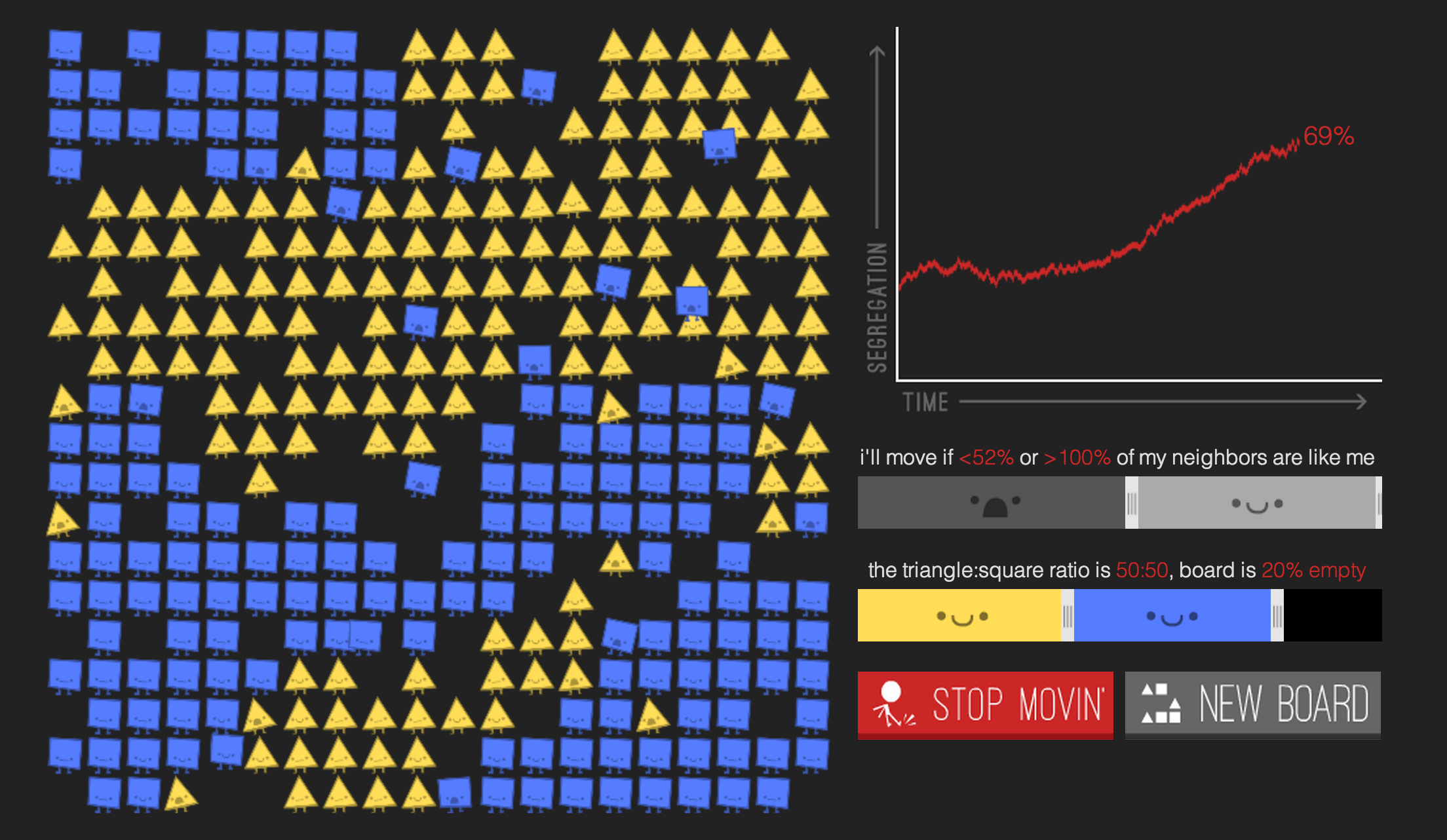
Most of my interest is in agent-based modeling rather than system dynamics, so I'll go into a little more depth here by walking through Schelling's model of segregation. This model was developed to demonstrate that even when individuals have "tolerant" preferences about who they live near, neighborhoods may in aggregate still end up segregated.

Every agent-based model has two core components: the agents and their environment.

In Schelling's model, agents are typically modeled as households, placed in a 2D grid environment. This is similar to cellular automata, like the Game of Life; CAs can be thought of as a subset of ABMs.

Each household has a "type" (typically representing race) and a tolerance threshold ¦t¦. This threshold defines the minimum amount (percent) of similar neighbors required for the household to be "satisfied". An unsatisfied household will move to a random unoccupied spot in the grid.

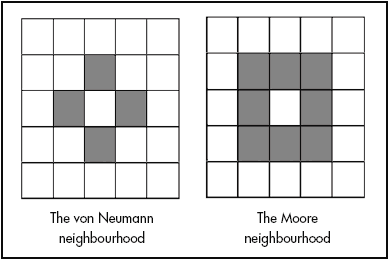
Here we consider Von Neumann neighbors; that is, the spaces to the north, east, west, and south of a cell. This is in contrast to a Moore neighborhood, which includes all eight surrounding cells.

Here's how an Schelling agent would be defined in System Designer (still under heavy development! The API will change!), an agent-based modeling framework Fei Liu and I are currently developing:

import syd
import numpy as np

class SchellingAgent(syd.Agent):
    state_vars = ['type', 'position', 'satisfied', 'threshold']

    async def decide(self):
        neighbors = await self.world.neighbors(self.state.position)
        same = np.where(neighbors == self.state.type)[0]
        satisfied = same.size/neighbors.size >= self.state.threshold
        self.submit_var_update('satisfied', satisfied)
        if not satisfied:
            await self.world.queue_random_move(self.state.position, self.state.type, self.addr)

And here's how the Schelling environment (world) would be defined:

import random

class SchellingWorld(syd.world.GridWorld):
    state_vars = ['grid', 'vacancies']

    async def decide(self):
        self.submit_update(self.update_vacancies)

    @syd.expose
    async def queue_random_move(self, position, agent_type, agent_addr):
        if self.state.vacancies:
            new_pos = self.state.vacancies.pop(random.randrange(len(self.state.vacancies)))
            self.submit_update(self.move_position, position, new_pos, agent_type)
            agent_proxy = await self.container.connect(agent_addr)
            await agent_proxy.submit_var_update('position', new_pos)

    def update_vacancies(self, state):
        state.vacancies = list(self.vacancies(empty_val=0))
        return state

Then, to run the simulation:

from itertools import product

n_types = 2
n_agents = 50
width = 10
height = 10
grid = np.zeros((width, height))
positions = list(product(range(width), range(height)))

# value of 0 is reserved for empty positions
types = [i+1 for i in range(n_types)]

sim = syd.Simulation(node)
world, world_addr = sim.spawn(SchellingWorld, state={'grid': grid, 'vacancies': []})

for _ in range(n_agents):
    position = positions.pop(0)
    type = random.choice(types)
    agent, addr = sim.spawn(SchellingAgent, state={
        'type': type,
        'position': position,
        'satisfied': 0.,
        'threshold': threshold
    }, world_addr=world_addr)
    syd.run(world.set_position(type, position))

    for report in sim.irun(n_steps, {
        'n_satisfied': (lambda ss: sum(s.satisfied for s in ss if hasattr(s, 'satisfied')), 1)
    }):
        print('mean satisfied:', report['n_satisfied']/n_agents)

One key question when developing an ABM is: what constitutes an agent? Is it an individual, a family, a firm, a city, a nation, a cell, a grain of sand, etc? That is, what scale is relevant for the simulation? Of course, this depends on the exact problem at hand, but one idea which is particularly interesting is multiscale simulations.

In video games there is this notion of "level-of-detail" (LOD). When you are very close up to an object in a game (say, a rock) the engine loads a very high-resolution texture or more complex mesh so you can see all its detail. If however you're looking at the rock from far away, you won't be able to see the fine details and so it would be a waste to load such a high-resolution texture. Instead, a low-resolution texture or lower-poly mesh can be loaded and you won't be able to tell the difference.

Maybe the same idea can be applied to agent-based modeling. If you are "zoomed out" you don't see the actions of individuals but instead, for example, cities. It's not as straightforward as it sounds but it has a lot of appeal.

ABMs and Machine Learning

How does machine learning factor into agent-based models? Many agent-based models are fairly simple, relying on hand-crafted rules, but they can get very sophisticated too.

For example, in our project Humans of Simulated New York, Fei and I wanted to generate "plausible" simulated citizens. To do so we used ACS PUMS data (individual-level Census data) to learn a Bayes net (a generative model) which would capture correlations present in the data (this generation code is available on GitHub).

For example we could generate a citizen "from scratch":

>>> from people import generate
>>> year = 2005
>>> generate(year)
{
    'age': 36,
    'education': <Education.grade_12: 6>,
    'employed': <Employed.non_labor: 3>,
    'wage_income': 3236,
    'wage_income_bracket': '(1000, 5000]',
    'industry': 'Independent artists, performing arts, spectator sports, and related industries',
    'industry_code': 8560,
    'neighborhood': 'Greenwich Village',
    'occupation': 'Designer',
    'occupation_code': 2630,
    'puma': 3810,
    'race': <Race.white: 1>,
    'rent': 1155.6864868468731,
    'sex': <Sex.female: 2>,
    'year': 2005
}

Or specify some value, e.g. generate me a person from a particular neighborhood. It's not perfect, but it worked well enough for our purposes.

Similarly, we used a logistic regression model trained to predict the probability of two people being confidants (from Social Distance in the United States: Sex, Race, Religion, Age, and Education Homophily among Confidants, 1985 to 2004, Jeffrey A. Smith, Miller McPherson, Lynn Smith-Lovin. University of Nebraska - Lincoln. 2014), using that to bootstrap the simulation's social network.

HOSNY also included businesses which produced and sold goods (including consumer good firms, which produced food, capital equipment firms, and raw material firms). They needed to decide how much of a good to produce and what to price it at. It's quite difficult to come up with a set of rules that will work well here, so we implemented them with Q-learning (as described in "An agent-based model of a minimal economy, a basic reinforcement learning algorithm (reinforcement learning algorithms are the class of techniques used by AlphaGo, for instance).

Similarly, we implemented the government as a reinforcement learning agent, using Q-learning to decide on tax rates.

These are just a few examples of where the fields of simulation and machine learning overlap.

A systems language

In The Image of the City, urban planner Kevin Lynch interviews people in multiple cities to understand how they form "mental maps" of their cities.

We rely on similar mental maps when navigating non-corporeal landscapes. In Postmodernism Fredric Jameson references The Image of the City when calling for improved versions of this "cognitive mapping". As he describes it:

a situational representation on the part of the individual subject to that vaster and properly unrepresentable totality which is the ensemble of society's structures as a whole

Jeff Kinkle quotes Jameson's discussion of alienation and mobility in particular:

Lynch taught us that the alienated city is above all a space in which people are unable to map (in their minds) either their own positions or the urban totality in which they find themselves. […] Disalienation in the traditional city, then, involves the practical reconquest of a sense of place and the construction or reconstruction of an articulated ensemble which can be retained in memory, and which the individual subject can map and remap along the moments of mobile, alternative trajectories.

Kinkle further notes:

an inability to cognitively map the mechanisms and contours of the world system is as debilitating politically as being unable to mentally map a city would be for a city dweller.

Can we, again quoting Kinkle quoting Jameson, develop a way of thinking about systems "so vast that [they] cannot be encompassed by the natural and historically developed categories of perception with which human beings normally orient themselves"? Is there any way to better represent these complex systems in which we are submerged, along with their incredibly nuanced causal chains, in a way that makes them more manageable and navigable?

How do we do so without relying on the crutch of conspiracy theories, inappropriately reducing the complexity of a situation in order to make it more comprehensible?

For cities we now have Google Maps. What about for these social systems?

This seemingly intractable problem has sometimes been called the "crisis of representation" or "representational breakdown". Speaking of climate change, but equally applicable to any similarly overwhelming problem:

What kinds of representation (visual and otherwise) are adequate to the task of conveying climate change, and perhaps most importantly, to stemming dysphoric paralysis while triggering critical thinking and action? (Archives of the Present-Future: On Climate Change and Representational Breakdown, Emily Eliza Scott)

There are many different ways of representing something like climate change. There isn't really a right one; they all have different effects.

For example: depicted here is a protest in the Maldives (which is at a very high risk of being submerged in the near future) where President Nasheed and his cabinet sent an SOS message to the UN climate change summit from underwater.

But what if we want to better comprehend the "total" system, with its interconnections, insofar as it even can be represented?

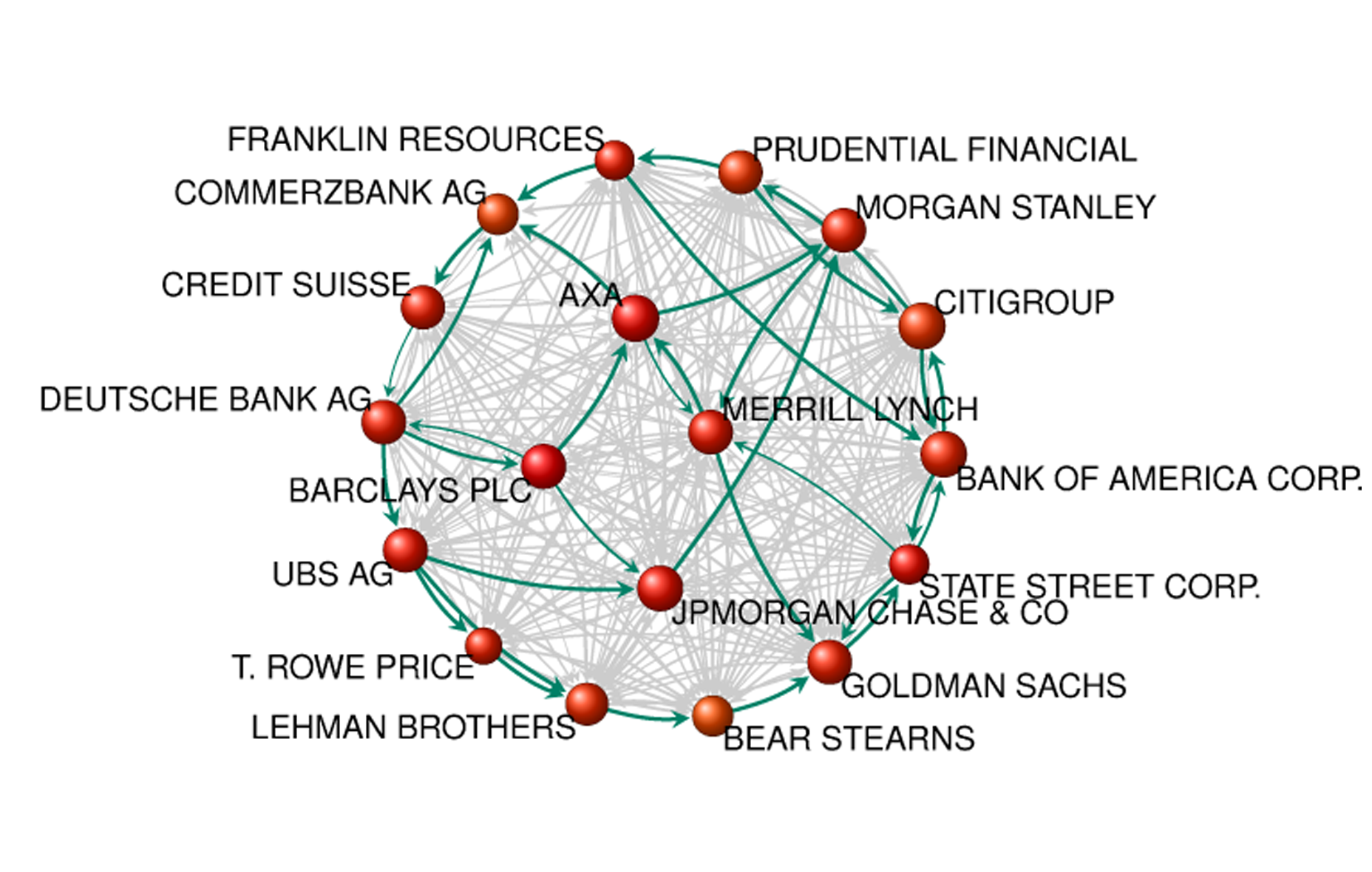
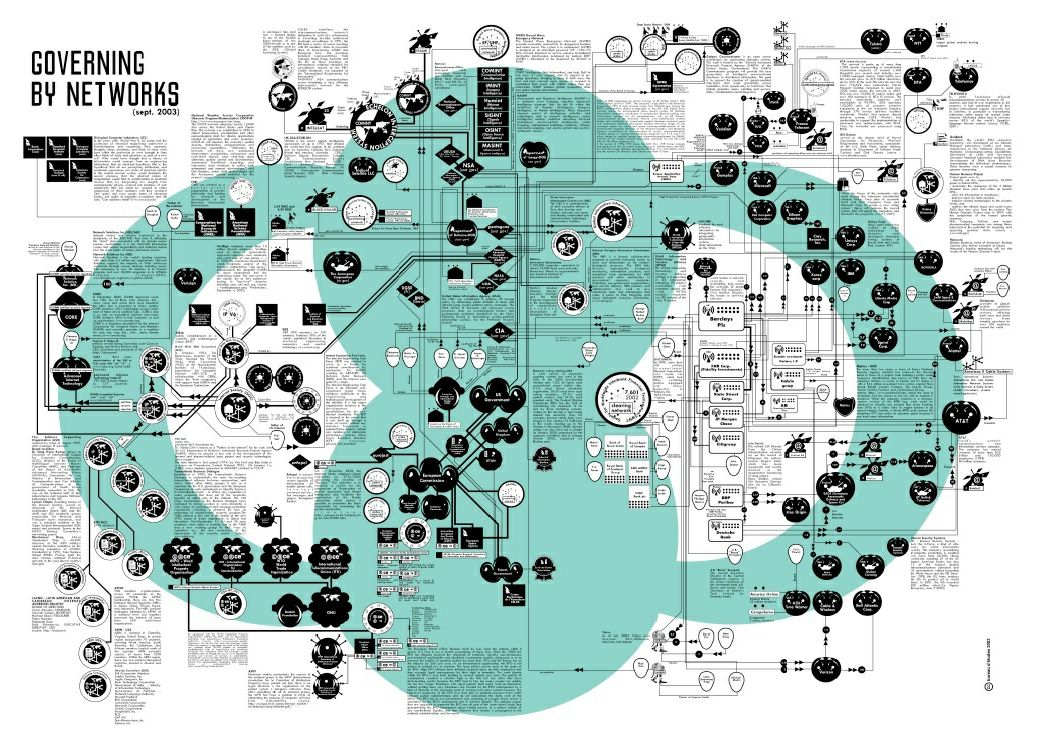
When it comes to systems the network is perhaps the most common type of representation. Networks are a fantastic abstract form but perhaps ineffective in communicating a system's less technical aspects. It is capable of describing the full system (in terms of its relational structure) but even this may serve only to intimidate. Such intimidation may be the only affective effect of such a representation, failing to depict the human experiences that emerge from and compel or resist the system.

For example, Bureau d'Etudes' An Atlas of Agendas is a meticulously researched mapping of organizations throughout the world, so detailed that a magnifying glass accompanies the book (they were originally produced at a larger scale on walls). It is undeniably impressive but induces vertigo and helplessness in its unmanageable intricacy.

This kind of network mapping also doesn't capture the dynamism of such a system.

In contrast to network mapping, Cartographies of the Absolute (the title is a direct reference to the aforementioned Jameson book), Jeff Kinkle and Alberto Toscano examine how narrative fiction provides a more experiential representation, i.e. an aesthetics, discussing for example The Wire and cinema from the peak of New York City's "planned shrinkage" (such as Wolfen). Kinkle describes the Cartographies of the Absolute project as such:

The project is an investigation into various attempts in the visuals arts to cognitively map the contours of the current world system and its influence on various local settings...focus[ing] on the techniques artists, filmmakers, and cartographers use to portray global forces in all their complexity without being merely didactic or reverting to antiquated aesthetic models.

For example, the chapter on The Wire, "Baltimore as World and Representation":

[The Wire] address[es] the drug trade, de-industrialization, city hall, the school system and the media...mapped both vertically (making internal hierarchies explicit) and horizontally (tracking their entanglements and conflicts with other 'worlds' spread throughout the city...we are...able to see how each world affects the ones around it...

This type of representation is more visceral and emotional but may obscure the totality of the underlying system (although The Wire seems to do a good job).

Is there some kind of representational "language" that falls in between? In Iain M. Bank's Culture novels he describes a language called "Marain" which "appeal[s] to poets, pedants, engineers and programmers alike". Is there an equivalent here, one that can similarly bridge the technical and the emotional representations, allowing the expressiveness of both?

In Ted Chiang's The Story of Your Life (which is being made into a movie now), a researcher studies an alien language which has two components - spoken (Heptapod A) and graphic (Heptapod B). The aliens tend to prefer the graphic one because the spoken language is limited by the arrow of time - it goes in one way and you have to "wait" to hear all or most of the sentence to grasp the meaning. With the graphic language, which I picture as large mandala-like ideograms, the whole sentence is consumed at once, there in front of you, which, for these aliens at least, lead to an instant and more total understanding of what was being communicated. Is there an analog of that for us?

In Thinking in Systems, Donella H. Meadows makes a similar observation:

there is a problem in discussing systems only with words. Words and sentences must, by necessity, come only one at a time in linear, logical order. Systems happen all at once.

... Pictures work for this language better than words, because you can see all the parts of a picture at once.

The possible impact of such a language in affecting our way of thinking can be seen in the effect of transitioning from Roman numerals to Hindu-Arabic numerals. Wilensky & Papert refer to these numeral systems as an example "representational infrastructure", calling this shift a "restructuration" which ultimately led to arithmetic being accessible to essentially everyone. Roman numerals were not amenable to - they did not afford, to use a design term - certain mathematical operations that are now second-nature to many; with Roman numerals only a specially-trained group of people could do such arithmetic. Wilensky is the creator of NetLogo, a very popular framework for agent-based modeling, so he seems to be positioning ABMs as a restructuration.

So what kind of language - what kind of representational infrastructure - is needed for everyone to be comfortable with complex systems?

Social simulation itself may not be this language, but it seems inevitable that it will at least be the engine for it. Perhaps we can build richer experiences on top of this engine.

A canvas for alternatives

Simulation can build an appreciation of the arbitrariness of the present, insofar as things could have played out different and still can play out differently ("another world is possible").

So many terrible systems and practices are maintained under the pretence of being "natural" (e.g. the infuriating "human nature" argument), so there we often see rhetoric justifying such arrangements along those lines; they are framed as spontaneous and organically-formed. They usually aren't, and even if they are, that's not a very convincing justification for their continuation.

This speculative aspect of simulation is really appealing; it carves out this space for experimentation and imagining utopias.

Fei Liu and I approached our project Humans of Simulated New York in this way. HOSNY was implemented as a simple economic simulation primarily based on New York City Census data, but we allowed people to play with the parameters of the world along three axes: food/agriculture, health, and technology/labor and see how the lives of citizens change in each alternate world.

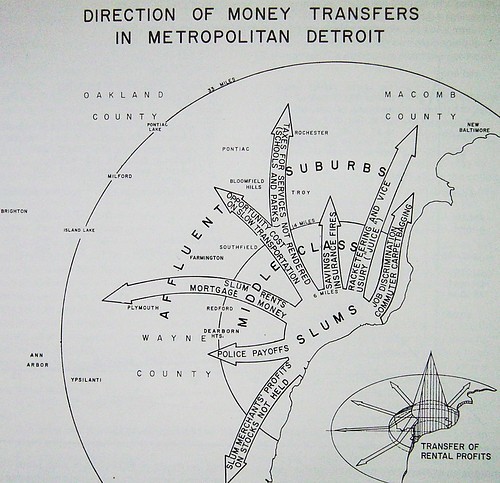
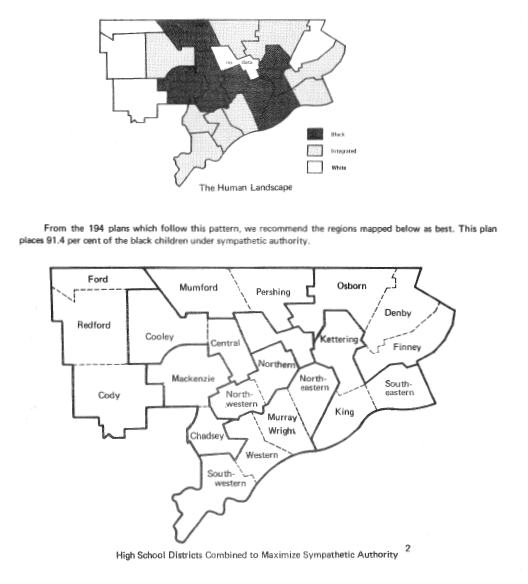
There is a parallel here to cartography - in the late 1960's and early 1970's The Detroit Geographical Expedition and Institute (DGEI) focused on producing "oughtness maps": "maps of how things are and maps of how things ought to be." (The Detroit Geographic Expedition and Institute: A Case Study in Civic Mapping, Catherine D'Ignazio). William Bunge, one of the co-founders of the DGEI (the other was Gwendolyn Warren), noted (probably referencing Marx):

Afterall, it is not the function of geographers to merely map the earth, but to change it.

I feel a similar sentiment can be said about simulation. Perhaps we can see the emergence of simulation equivalents of the practices of "countermapping" and "radical cartography".

Exploring policy-space

This kind of systems mapping and modeling has more "practical" applications. For example, identifying points of influence/leverage points within a network.

One area of interest is in public policy modeling. The way policy is handled now seems totally nonsensical, and of course there is more than just ignorance about consequences to blame (i.e. politics), but I wonder if this sort of modeling wouldn't have at least some positive impact.

A comprehensive textbook on the topic, Modeling Complex Systems for Public Policies, was published last year so it seems like a fairly active area of research. In the text researchers discuss modeling transit systems, education systems, economies, cities,

One active and ambitious initiative in this area is the Eurace@Unibi model. It's a joint venture involving multiple European research institutes and seeks "to provide a micro-founded macroeconomic model that can be used as a unified framework for policy analysis in different economic policy areas and for the examination of generic macroeconomic research questions." (The Eurace@Unibi Model: An Agent-Based Macroeconomic Model for Economic Policy Analysis) The goal is to develop an economic model that has more representative power than existing methods (i.e. dynamic stochastic general equilibrium, or DSGE models, which, as the name suggests, are focused on equilibriums) and so would be a better tool for determining economic policy. I don't have enough experience with the model or economics itself to really comment on its relative effectiveness, but it's interesting nonetheless.

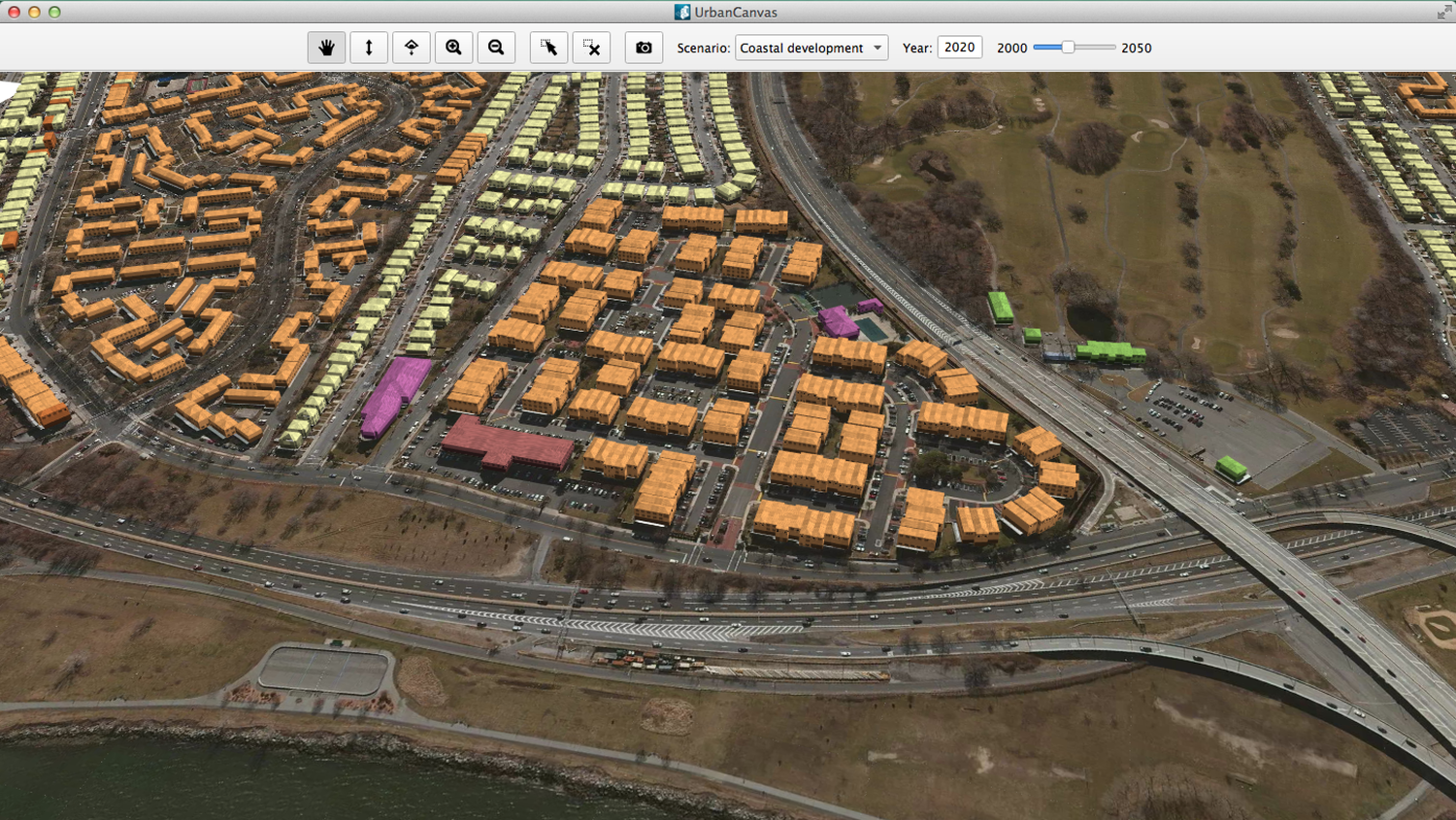
In urban planning a similar initiative exists, UrbanSim, an "open source simulation platform for supporting planning and analysis of urban development, incorporating the interactions between land use, transportation, the economy, and the environment."

There is an important distinction that needs to be brought up here: speculation vs prediction. Such an application of social simulation is not about predicting the outcome of a policy but rather about understanding what the possibilities are.

I try to mention this point a lot because social simulation is often misconstrued as something like Asimov's "psychohistory", which is described as a means of predicting the trajectories of civilizations.

Bret Victor, in What can a technologist do about climate change?, puts it this way:

Modeling leads naturally from the particular to the general. Instead of seeing an individual proposal as “right or wrong”, “bad or good”, people can see it as one point in a large space of possibilities. By exploring the model, they come to understand the landscape of that space, and are in a position to invent better ideas for all the proposals to come. Model-driven material can serve as a kind of enhanced imagination.

Scott E. Page makes a similar caveat in the preface to Modeling Complex Systems for Public Policies:

Complex systems do not represent a silver bullet, but another arrow in the policy maker's quiver. More accurately, all of these tools put together can be thought of as multiple imperfect arrows that provide insight into what is likely to happen, what could happen, and how what happens might spill into other domains.

That is, simulation is more about counterfactuals (what-ifs), laying out the possibility space and shining a light on more of it than we would without such tools. It's not about predicting anything, but about exploring and speculating and moving towards understanding.

In any case, this application of simulation induces anxiety...there are too many examples of technology amplifying the power of those who already have too much of it. It's a common topic in science fiction: in the miniseries World on a Wire (which shares the source material behind The Thirteenth Floor but is quite a different experience), the IKZ (Institute for Cybernetics and Future Science) is pressured to use their simulated world to predict steel prices for the steel industry.

This furthers the urgency of popularizing this way of thinking. As we're seeing with the proliferation of machine learning, such technological vectors of control are especially potent when the public don't have opportunities to learn how they work.

A means for discourse

One side effect of translating mental models into simulation code is that you generally need to render your assumptions explicit. One assumptions are made unambiguous in code, it is easier to point to them, discuss them, and perhaps modify them. You can fork the model and assert your own perspective.

This becomes clear when you look at games which rely on simulation, like SimCity. As Ava Kofman points out in Les Simerables:

To succeed even within the game’s fairly broad definition of success (building a habitable city), you must enact certain government policies. An increase in the number of police stations, for instance, always correlates to a decrease in criminal activity; the game’s code directly relates crime to land value, population density, and police stations. Adding police stations isn’t optional, it’s the law.

Chris Franklin (Errant Signal) similarly notes many problematic assumptions in Civilization 5, such as framing only certain societies as "civilizations" (the rest are "barbarians", which are literally under the same banner as wild animals), and further asserting that the only valid form of social organization and actor in history is the nation-state. As such it precludes the possibility of alternative forms of society; the game simulation leaves no space for such things.

These two instances could be framed as examples of what Ian Bogost calls "procedural rhetoric", defined as:

an argument made by means of a computer model. A procedural rhetoric makes a claim about how something works by modeling its processes in the process-native environment of the computer rather than using description (writing) or depiction (images). (Persuasive Games: The Proceduralist Style, Ian Bogost)

Another example includes molleindustria's Nova Alea, a game about speculative real estate investment and gentrification in which you pump money into a city block to (if all goes well) see it grow and later reap the profits.

I'm also developing a video game, The Founder: A Dystopian Business Simulator, which argues that the logic that compels Silicon Valley is inherently destructive and destabilizing. In it you found and manage a startup for as long as you can satisfy the required growth targets. Maintaining growth requires hiring cheap labor, replacing it where possible, commingling with the government, pacifying employees, and more.

With simulation the mechanics of a system as you see it must be laid bare. They become components which others can add to or take from or rearrange and demonstrate their own perspective. This is no doubt utopian of me to say, but I would love to see a culture of argumentation via simulation!

Exploration & education

Simulations can be used to argue, but they can also be used for education, falling under the rubric of "explorable explanations". That is, when imbued with interactivity, simulations can essentially function as powerful learning tools where the process of exploration is similar to or indistinguishable from play.

Nicky Case is doing a lot of amazing work here. Their projects are great at communicating the pedagogical appeal of simulation. Parable of the Polygons (developed with Vi Hart) is a wonderful presentation of Schelling's segregation model. Their emoji simulation prototype is also awesome. (I highly recommend their talk How to Simulate the Universe in 134 Easy Steps.

Nicky also maintains a collection of explorable explanations, framing them as such:

What if a book didn't just give you old facts, but gave you the tools to discover those ideas for yourself, and invent new ideas? What if, while reading a blog post, you could insert your own knowledge, challenge the author's assumptions, and build things the author never even thought of... all inside the blog post itself?

What if, in a world where we're asked to constantly consume knowledge, we construct knowledge?

Working off a similar strand of thought is Buckminster Fuller's proposed "World Game":

In the 1960's Buckminster Fuller proposed a “great logistics game” and “world peace game” (later shortened to simply, the “World Game”) that was intended to be a tool that would facilitate a comprehensive, anticipatory, design science approach to the problems of the world. The use of “world” in the title obviously refers to Fuller's global perspective and his contention that we now need a systems approach that deals with the world as a whole, and not a piece meal approach that tackles our problems in what he called a “local focus hocus pocus” manner. (Buckminster Fuller Institute)

I loved this idea of a shared game through which people learn to think on a global scale, about the interrelatedness of all things, imbuing an acknowledgement of our connectedness as a species from a young age.

It reminds me of the fictional game Azad, from The Player of Games, which is played annually by the Empire of Azad and literally dictates how the civilization is run and what it values as a culture. The game has enough depth and complexity that a player can reflect their entire philosophy and perspective about the world through how they play. It's a beautiful capacity for a game to aspire to.

As far as I know Fuller's World Game never materialized, but a game which seems to trace its intellectual lineage to this proposal is Strange Loop Games' ECO, where players must collaborate in a simulated ecosystem to build a lasting society, involving both an player-run economy and a government, and culminating in cooperating to prevent an extinction event (a meteor impact).

Looking forward into the future, the speculative paper Optimists’ Creed: Brave New Cyberlearning, Evolving Utopias (Circa 2041) (Winslow Burleson & Armanda Lewis) postulates an educational method called "cyberlearning" which integrates VR, AI, and simulation:

Cyberlearning provides us (1) access to information and (2) the capacity to experience this information’s implications in diverse and visceral ways. It helps us understand, communicate, and engage productively with multiple perspectives, promoting inclusivity, collaborative decision-making, domain and transdisciplinary expertise, self actualization, creativity, and innovation (Burleson 2005) that has transformative societal impact.

This is the holy grail of simulation to me - such an educational experience could have an incredible effect.

MIT's CityScope project is a step in this direction, providing an interactive "Tactile Matrix" - a city in the form of Legos - that is connected to an urban simulation.

Experience generation

Last but not least: experience generation. Earlier I asked how we imbue simulation with the narrative richness other media provides. That is, how do we more accurately communicate the experiences that a simulation might (ostensibly) represent?

Humans of Simulated New York tries to tackle this question. We were initially curious about "breathing life" into data. Data about human phenomenon are meant to translate experiences into numbers which may reveal something about the underlying structure of these phenomenon. Perhaps if we take this structure, parameterized with these numbers, we can use simulation to generate some experience which better approximates the experience that initially generated the data.

Many "experience generators" already exist. Video games are probably the most ubiquitous example. Games like Kentucky Route Zero and Gone Home are powerful ways of telling the stories of individuals.

These particular examples at least are highly-scripted narratives; ultimately they are very guided and linear.

Some games go beyond this by not writing a particular story but instead defining the world in which many stories can happen. Games of this category include Cities: Skylines, Stellaris (similar to a galactic Civilization game), and famously Dwarf Fortress. These games describe rules for how a world (or universe) works and provides players the space to create their own stories.

These games, however, are not derived from real-world data and, perhaps as a result of this, lack the same narrative power that games like Gone Home have. It seems like if we can create game from a simulation meant to approximate our society (at least the aspects relevant to the stories we wish to tell) we can create a deeply engaging way to learn about each other. Sort of like Fuller's World Game, but one that doesn't privilege the global perspective and equally appreciates the individual one.

We certainly did not achieve this with HOSNY but this is part of what motivated the project. We were interested in creating a simulation that modeled a typical day in the life of a New Yorker of a particular demographic, as described by Census data (in particular, New York City American Community Survey data spanning 2005-2014). The following sketch gives an idea:

The simulation agents ("simulants") had very simple behaviors. They needed to buy food for them and their family and, unless they were independently wealthy or a business owner, had to find employment to get the money to do so. They also had to pay rent, could get sick, could visit the doctor if they could afford it, and could start a business if they could afford it. They also varied a bit in personality - this part was totally separate from the dataset - which influenced their decision making.

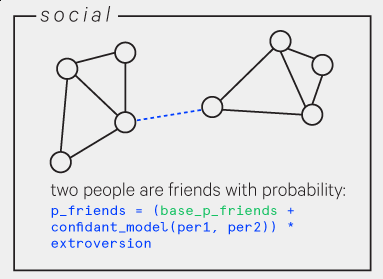
A social simulation needs a social network so we used a model from Social Distance in the United States: Sex, Race, Religion, Age, and Education Homophily among Confidants, 1985 to 2004 (Jeffrey A. Smith, Miller McPherson, Lynn Smith-Lovin. University of Nebraska - Lincoln. 2014) which looked at what factors correlated with two people being confidants. Given two simulants, this model output a probability that they would be friends.

The full simulation design document is available here.

The end result was a participatory economic simulation which players, after joining via their phone, are assigned a random simulant. It's their duty to ensure the well-being of their simulant by voting on and proposing legislation they believe will help improve their life.

I don't think we quite achieved generating a compelling narrative with this particular project, but I do think the general methods used will eventually support a successful one.

System Designer (SyD)

Fei and I are working on a framework, System Designer (SyD for short), which tries to tie together and realize these ideas I've discussed here. The goal is to create an accessible tool for constructing, running, and playing with social simulations and develop an accompanying educational program.

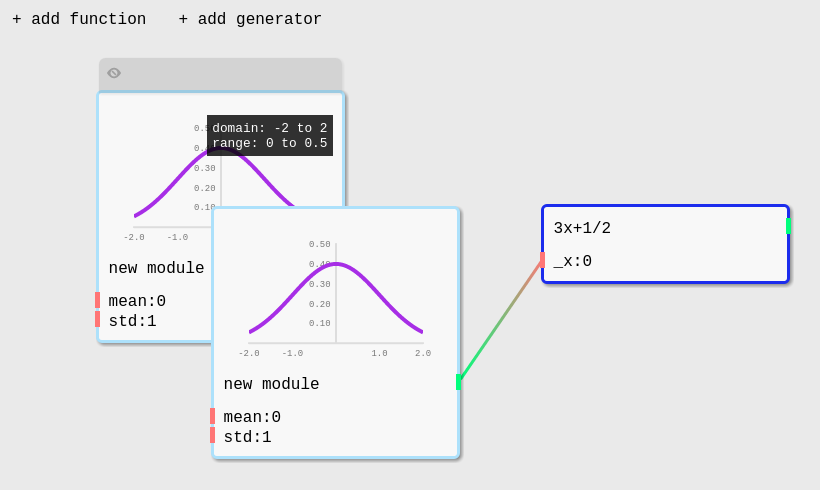
Our current blurb for describing it:

An open-source simulation toolkit and conceptual framework to make complex systems thinking (how did we get here/where are we now?) and the simulation of alternative worlds (where can we go?) more accessible to designers, activists, urban planners, educators, artists....

The framework is still in its early stages, but the plan is to include:

• an engine for running simulations (Python)
  • multi-node support
  • extensibility
  • common data format for sharing/forking models
• a protocol for communicating with the engine
  • to build arbitrary interfaces to build & tweak simulations
  • to build arbitrary visualizations on top
• a GUI editor for building/tweaking simulations
• workshops to teach the method & tool

Wrap up and come down

Clearly I'm very excited about the possibilities here, but I also want to add as a caveat: I'm not advocating this as some monolithic silver bullet (even though it might sound that way). I think simulation (in particular, agent-based modeling and system dynamics) is a very interesting methodology that has an inherent appeal and provides powerful new ways of looking at the world. But I also have reservations and uncertainties which I would be happy to discuss afterwards. There is one main concern I want to address, and it basically amounts to: "how well can we actually model people?"

This is a difficult question that has many different phrasings and different answers for some and no answers for others.

As a general and perhaps unsatisfying answer, I don't, at my current level of understanding of the field, think we can ever model people "perfectly" or even at an extremely high-fidelity (perhaps due to a combination of limits of computation and of what we can understand about human behavior generally), but I do think we can model people at a convincing and useful level. To quote George Box (this quote had to be in here somewhere): "all models are wrong, but some are useful".

The promise/spectacle of big data has revived a notion of "social physics", the idea that we can describe immutable laws which govern human behavior. In fact, Bruno Latour seems to be arguing for the abandonment of methods like agent-based modeling in favor of big-data-driven social science. Most of us are familiar with how flawed the idea of "big data == truth" is (Nathan Jurgenson goes into more detail about the shortcomings here), but to put it succinctly: processes of data collection and analysis are both subject to bias, and the "infallible big-data" rhetoric completely blinds practitioners to it.

In 2014, Joshua Epstein published Agent_Zero: Toward Neurocognitive Foundations for Generative Social Science. It is an ambitious attempt at defining a "first principles" agent that models what he describes as the three core components to human behavior: the cognitive (rational), the affective (emotional), and the social. The book is fascinating and I think there is a lot to be learned from it, but it also needs to be considered with great care because it too seems subjectable to a biased understanding of what constitutes human behavior.

Of course, there is no methodology that is immune to potential bias, and as Jurgenson notes in View from Nowhere, the main safeguard is training practitioners to recognize and mitigate such bias as much as possible. The same caveat needs to be applied to the methods of social simulation, and even so, I still believe them to hold a great deal of promise that needs to be further explored.

occhiolism
n. the awareness of the smallness of your perspective, by which you couldn't possibly draw any meaningful conclusions at all, about the world or the past or the complexities of culture, because although your life is an epic and unrepeatable anecdote, it still only has a sample size of one, and may end up being the control for a much wilder experiment happening in the next room.

from the dictionary of obscure sorrows

In Free to Choose, Milton Friedman presents a pencil (the idea is borrowed from a poem) in order to sort of marvel at the wonder of the free market, how all these disparate people and resources were coordinated to produce something as simple as a pencil, and he's sort of coming from the angle of it's great because you don't have to think about that production process at all, it's totally abstracted away from you, and he doesn't seem to be interested in acknowledging how fraught the politics of production is (or maybe he just doesn't care).

Is there a way to do the opposite? To make the production process of say your smartphone - conflict mining and poor working conditions and publicly-funded research and so on - undeniably obvious in the object itself? To really make that whole production network felt ("real") to the end user? And going a step further, what happens after the consumer is done with it? For example, e-waste dumps in Ghana and China.

Sourcemap maps out the supply chains of various products and I wonder what can be built on top of it.

As part of my OpenNews fellowship I have been catching up on the theory behind machine learning and artificial intelligence. My fellowship is ending soon, so today I'm releasing the notes from the past year study to bookend my experience.

To get a good grasp of a topic, I usually went through one or two courses on it (and a lot of supplemental explanations and overviews). Some courses were fantastic, some were real slogs to get through - teaching styles were significantly different.

The best courses has a few things in common:

1. introduce intuition before formalism
2. provide convincing motivation before each concept
3. aren't shy about providing concrete examples
4. provide an explicit structure of how different concepts are hierarchically related (e.g. "these techniques belong to the same family of techniques, because they all conceptualize things this way")
5. provide clear roadmaps through each unit, almost in a narrative-like way

The worst courses, on the other hand:

1. lean too much (or exclusively) on formalism
2. seem allergic to concrete examples
3. sometimes take inexplicit/unannounced detours into separate topics
4. just march through concepts without explaining how they are connected or categorized

Intuition before formalism

In machine learning, how you represent a problem or data is hugely important for successfully teaching the machine what you want it to learn. The same is, of course, for people. How we encode concepts into language, images, or other sensory modalities is critical to effective learning. Likewise, how we represent problems - that is, how we frame or describe them - can make all the difference in how easily we can solve them. It can even change whether or not we can solve them.

One of the courses I enjoyed the most was Patrick Winston's MIT 6.034 (Fall 2010): Artificial Intelligence. He structures the entire course around this idea of the importance of the right representation and for people, the right representation is often stories (he has a short series of videos, How to Speak, where he explains his lecturing methods - worth checking out).

Many technical fields benefit from presenting difficult concepts as stories and analogies - for example, many concepts in cryptography are taught with "Alice and Bob" stories, and introductory economics courses involve a lot of hypothetical beer and pizza. For some reason concepts are easier to grasp if we anthropomorphize them or otherwise put them into "human" terms, anointing them with volition and motivations (though not without its shortcomings). Presenting concepts as stories is especially useful because the concept's motivation is often clearly presented as part of the story itself, and they function as concrete examples.

Introducing concepts as stories also allows us to leverage existing intuitions and experiences, in some sense "bootstrapping" our understanding of these concepts. George Polya, in his Mathematics and Plausible Reasoning, argues that mathematical breakthroughs begin outside of formalism, in the fuzzy space of intuition and what he calls "plausible reasoning", and I would say that understanding in general also follows this same process.

On the other hand, when concepts are introduced as a dense mathematical formalism, it might make internal sense (e.g. "¦a¦ has this property so naturally it follows that ¦b¦ has this property"), but it makes no sense in the grander scheme of life and the problems I care about. Then I start to lose interest.

Concept hierarchies

Leaning on existing intuition is much easier when a clear hierarchy of concepts is presented. Many classes felt like, to paraphrase, "one fucking concept after another", and it was hard to know where understanding from another subject or idea could be applied. However, once it's made clear, I can build of existing understanding. For instance: if I'm told that this method and this method belongs to the family of Bayesian learning methods, then I know that I can apply Bayesian model selection techniques and can build off of my existing understandings around Bayesian statistics. Then I know to look at the method or problem in Bayesian terms, i.e. with the assumptions made in that framework, and suddenly things start to make sense.

Some learning tips

Aside from patience and persistence (which are really important), two techniques I found helpful for better grasping the material were explaining things to other and reading many sources on the same concept.

Explain things to other people

When trying to explain something, you often reveal your own conceptual leaps and gaps and assumptions and can then work on filling them in. Sometimes it takes a layperson to ask "But why is that?" for you to realize that you don't know either.

Most ideas are intuitive if they are explained well. They do not necessarily need to be convoluted and dense (though they are often taught this way!). If you can explain a concept well, you understand it well.

Read a lot

People conceptualize ideas in different ways, relating them to their own knowledge and experiences. A concept really clicks if someone with a similar background to yours explains it because the connections will be more intuitive.

The same concepts are often present in many different fields. They may be referred to by different names or just have different preferred explanations. Seeing a concept in different contexts and introduced in different ways can provide a really rich understanding of it. If you can explain a concept in many different terms, you probably have a strong multi-perspective understanding of it.

The go-to rebuttal to increasing automation tends to be something around how creativity could not be emulated by computers, at least, not for awhile. There's some truth to that statement depending on how you define "creativity", I suppose. The least charitable definition might be synonymous with "content generation", a domain typically exclusive to humans - artists, musicians, writers, and so on - but computers have made some claim to this territory.

The poster child of the automated (i.e. procedural) content generation beachhead is No Man's Sky, which generates a literal universe, complete with stars and beaches and creatures, using interweaving mathematical equations. The universe it generates will reportedly take 5 billion years to explore, and that's just one of those universes. In theory, an infinite amount of universes can be generated by setting different seed values (the value which is used to determine all other values in the game). This interview with Sean Murray goes a bit more into depth on their approach.

These procedurally-generated universes aren't random, though they are designed to give that appearance. They are completely deterministic depending on the seed value - this is a critical property since there needs to be consistency. If you leave a planet, you should not only be able to come back to that planet, but it should be in a similar state to when you left it.

A big challenge in procedural content generation is figuring out a way of creating things which feel organic and natural - for No Man's Sky, the solution is the impressive-sounding Superformula, developed by John Gielis in 2003. In polar coordinates, with radius ¦r¦ and angle ¦\varphi¦, parameterized by ¦a, b, m, n_1, n_2, n_3¦, the Superformula is:

$$
r\left(\varphi\right) =
\left(
\left|
\frac{\cos\left(\frac{m\varphi}{4}\right)}{a}
\right| ^{n_2}
+
\left|
\frac{\sin\left(\frac{m\varphi}{4}\right)}{b}
\right| ^{n_3}
\right) ^{-\frac{1}{n_{1}}}.
$$

The above is the formula for two dimensions, but it is easily generalized to higher dimensions as well by using spherical products of superformulas (cf. Wikipedia).

Some forms resulting from the 2D formula:

Procedural generation is a really beautiful approach to game design. It's not so much about creating a specific experience but rather about defining the conditions for limitless experiences. No Man's Land is far from the first to do this, but it is the first (as far as I know) to have all of its content procedurally generated. The game Elite (from 1984!) also had procedurally-generated universe. Elite's universe was much simpler of course, but used a clever approach using the Fibonacci sequence to simulate randomness:

$$
\begin{aligned}
x_0 &= \text{seed} \
x_n &= x_{n-1} + x_{n-2}
\end{aligned}
$$

And then taking the last few digits of values generated from this sequence.

For example, take the Fibonacci sequence:

$$
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, \dots
$$

Let's jump at head in the sequence:

$$
1597, 2584, 4181, 6765, 10946, 17711, 28657, \dots
$$

If we just look at the last three digits, the resulting sequence looks quite random:

$$
597, 584, 181, 765, 946, 711, 657, \dots
$$

The great thing about this is that these universes can be shared by sharing seed values.

Procedural content generation is interesting, but other games focus on "procedural" stories. These games have (some) manually generated content - creatures, buildings, etc - but focus on designing complex systems which form the bedrock of the game's ability to spawn wild and fantastic stories. Dwarf Fortress and RimWorld are two great examples, which are essentially fantasy and sci-fi world-simulators (respectively) which model things like each individual's mental health, weather patterns, crop growth, and so on. No one writes the stories ahead of time, no one has a premeditated experience for you put in place - it's all off-the-cuff based on the dynamics of the game's rules.

The stories that come out of these games are amazing. Dwarf Fortress has an especially vibrant community based around the often absurd things that happen in game (for example, see r/dwarffortress, or for a more academic treatment, see Josh Diaz's thesis).

With the independent game industry continually expanding, I think we'll see more of these kinds of games. They can be developed with relatively small teams but have the richness and depth (and often to a better degree) of a massively-built studio game.

As part of the Coral Project, we're trying to come up with some interesting and useful metrics about community members and discussion on news sites.

It's an interesting exercise to develop metrics which embody an organization's principles. For instance - perhaps we see our content as the catalyst for conversations, so we'd measure an article's success by how much discussion it generates.

Generally, there are two groups of metrics that I have been focusing on:

• Asset-level metrics, computed for individual articles or whatever else may be commented on
• User-level metrics, computed for individual users

For the past couple of weeks I've been sketching out a few ideas for these metrics:

• For assets, the principles that these metrics aspire to capture are around quantity and diversity of discussion.
• For users, I look at organizational approval, community approval, how much discussion this user tends to generate, and how likely they are to be moderated.

Here I'll walk through my thought process for these initial ideas.

Asset-level metrics

For assets, I wanted to value not only the amount of discussion generated but also the diversity discussions. A good discussion is one in which there's a lot of high-quality exchange (something else to be measured, but not captured in this first iteration) from many different people.

There are two scores to start:

• a discussion score, which quantifies how much discussion an asset generated. This looks at how much people are talking to each other as opposed to just counting up the number of comments. For instance, a comments section in which all comments are top-level should not have a high discussion score. A comments section in which there are some really deep back-and-forths should have a higher discussion score.
• a diversity score, which quantifies how many different people are involved in the discussions. Again, we don't want to look at diversity in the comments section as a whole because we are looking for diversity within discussions, i.e. within threads.

The current sketch for computing the discussion score is via two values:

• maximum thread depth: how long is the longest thread?
• maximum thread width: what is the highest number of replies for a comment?

These are pretty rough approximations of "how much discussion" there is. The idea is that for sites which only allow one level of replies, a lot of replies to a comment can signal a discussion, and that a very deep thread signals the same for sites which allow more nesting.

The discussion score of a top-level thread is the product of these two intermediary metrics:

$$
\text{discussion score}{\text{thread}} = \max(\text{thread}}) \max(\text{thread}_{\text{width}})
$$

The discussion score for the entire asset is the value that answers this question: if a new thread were to start in this asset, what discussion score would it have?

The idea is that if a section is generating a lot of discussion, a new thread would likely also involve a lot of discussion.

The nice thing about this approach (which is similar to the one used throughout all these sketches) is that we can capture uncertainty. When a new article is posted, we have no idea how good of a discussion a new thread might be. When we have one or two threads - maybe one is long and one is short - we're still not too sure, so we still have a fairly conservative score. But as more and more people comment, we begin to narrow down on the "true" score for the article.

More concretely (skip ahead to be spared of the gory details), we assume that this discussion score is drawn from a Poisson distribution. This makes things a bit easier to model because we can use the gamma distribution as a conjugate prior.

By default, the gamma prior is parameterized with ¦k=1, \theta=2¦ since it is a fairly conservative estimate to start. That is, we begin with the assumption that any new thread is unlikely to generate a lot of discussion, so it will take a lot of discussion to really convince us otherwise.

Since this gamma-Poisson model will be reused elsewhere, it is defined as its own function:

def gamma_poission_model(X, n, k, theta, quantile):
    k = np.sum(X) + k
    t = theta/(theta*n + 1)
    return stats.gamma.ppf(quantile, k, scale=t)

Since the gamma is a conjugate prior here, the posterior is also a gamma distribution with easily-computed parameters based on the observed data (i.e. the "actual" top-level threads in the discussion).

We need an actual value to work with, however, so we need some point estimate of the expected discussion score. However, we don't want to go with the mean since that may be too optimistic a value, especially if we only have a couple top-level threads to look at. So instead, we look at the lower-bound of the 90% credible interval (the 0.05 quantile) to make a more conservative estimate.

So the final function for computing an asset's discussion score is:

def asset_discussion_score(threads, k=1, theta=2):
    X = np.array([max_thread_width(t) * max_thread_depth(t) for t in threads])
    n = len(X)

    k = np.sum(X) + k
    t = theta/(theta*n + 1)

    return {'discussion_score': gamma_poission_model(X, n, k, theta, 0.05)}

A similar approach is used for an asset's diversity score. Here we ask the question: if a new comment is posted, how likely is it to be a posted by someone new to the discussion?

We can model this with a beta-binomial model; again, the beta distribution is a conjugate prior for the binomial distribution, so we can compute the posterior's parameters very easily:

def beta_binomial_model(y, n, alpha, beta, quantile):
    alpha_ = y + alpha
    beta_ = n - y + beta
    return stats.beta.ppf(quantile, alpha_, beta_)

Again we start with conservative parameters for the prior, ¦\alpha=2, \beta=2¦, and then compute using threads as evidence:

def asset_diversity_score(threads, alpha=2, beta=2):
    X = set()
    n = 0
    for t in threads:
        users, n_comments = unique_participants(t)
        X = X | users
        n += n_comments
    y = len(X)

    return {'diversity_score': beta_binomial_model(y, n, alpha, beta, 0.05)}

Then averages for these scores are computed across the entire sample of assets in order to give some context as to what good and bad scores are.

User-level metrics

User-level metrics are computed in a similar fashion. For each user, four metrics are computed:

• a community score, which quantifies how much the community approves of them. This is computed by trying to predict the number of likes a new post by this user will get.
• an organization score, which quantifies how much the organization approves of them. This is the probability that a post by this user will get "editor's pick" or some equivalent (in the case of Reddit, "gilded", which isn't "organizational" but holds a similar revered status).
• a discussion score, which quantifies how much discussion this user tends to generate. This answers the question: if this user starts a new thread, how many replies do we expect it to have?
• a moderation probability, which is the probability that a post by this user will be moderated.

The community score and discussion score are both modeled as gamma-Poission models using the same function as above. The organization score and moderation probability are both modeled as beta-binomial models using the same function as above.

Time for more refinement

These metrics are just a few starting points to shape into more sophisticated and nuanced scoring systems. There are some desirable properties missing, and of course, every organization has different principles and values, and so the ideas presented here are not one-size-fits-all, by any means. The challenge is to create some more general framework that allows people to easily define these metrics according to what they value.